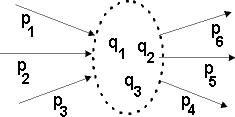
Die Vierer-Impulse  der äußeren Linien (p
1
,
p
2
, p
3
, ...) und inneren Linien (q
1
,
q
2
, q
3
, ...) werden nummeriert (siehe Abbildung rechts oben).
der äußeren Linien (p
1
,
p
2
, p
3
, ...) und inneren Linien (q
1
,
q
2
, q
3
, ...) werden nummeriert (siehe Abbildung rechts oben).
Zu jeder Wechselwirkung eines Vertex gehört ein Faktor g ~  ,
wobei
a
die
Kopplungskonstante der zugehörigen Wechselwirkung bezeichnet. Für jeden Vertex wird
daher ein Faktor
-ig
(mit dem komplexen i) notiert. ,
wobei
a
die
Kopplungskonstante der zugehörigen Wechselwirkung bezeichnet. Für jeden Vertex wird
daher ein Faktor
-ig
(mit dem komplexen i) notiert.
Für jede interne Linie, d.h. für jedes virtuelle Teilchen, wird ein Faktor der Form 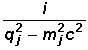
Für jeden Vertex kommt eine (Dirac`sche) Deltafunktion ( d (...)) folgender Form hinzu: Für jede interne Linie wird ein Faktor der Form 
Nach der Integration wird der Term eine Deltafunktion der Form (2 p ) 4 . d 4 (p 1 + p 2 + p 3 + ... - p n ) enthalten, die über die Impuls- und Energieerhaltung "wacht". Sie wird jetzt gestrichen. Der ganze Ausdruck ist gleich -i M zu setzen.
|
||||||||||||